Dijkstra -

Intuition

How do you find the shortest path from your home to your work in the city map? (assuming distance as only factor)

Dijkstra calculates this, but requires an “adjacency list” (check below section).

Algorithm idea

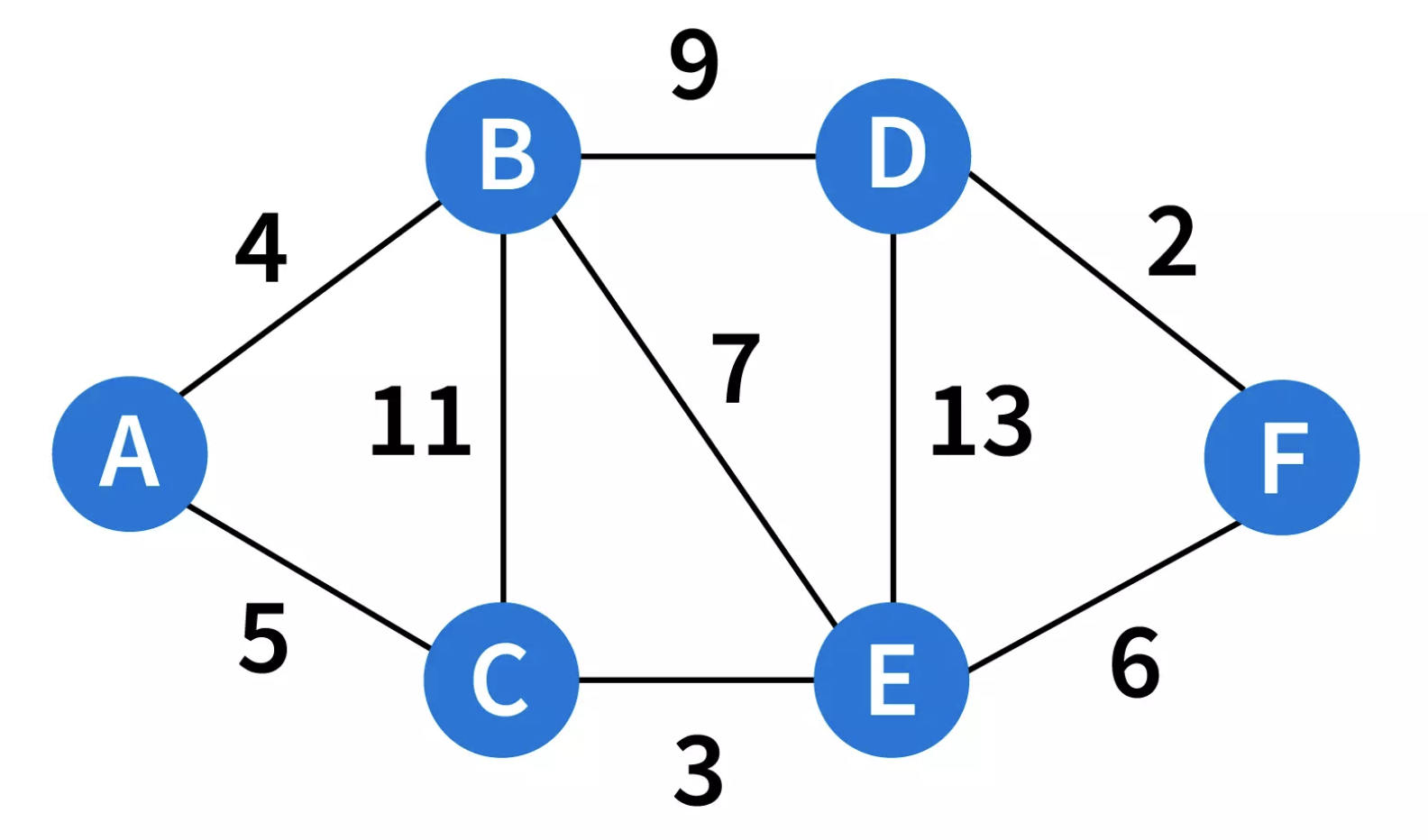
Dijkstra

Dijkstra calculates the minimum distance from an origin vertex (e.g. A) to EVERY vertex in the graph!
Start with direct edges: min distance to B = 4, min distance to C = 5. Keep track of these min distances in a dict.
As you check indirect edges (e.g. B -> E), the min distance is now B -> E (7) + min distance to B (4) = 11.
As you traverse, you might find more than one result for a vertex. Greedily overwrite min distances with lowest. Done 💥!

Algorithm

# Time: O((V+E)*logV)
# Space: O(V)
def dijkstra(
    adjacency: dict[int, list[list[int]]],
    num_vertices: int, # != len(adjacency) if there are orphan vertices!!
    start_vertex: int
) -> list[int]:
    # We start with default assumption that distance from start_vertex to every vertex
    # is infinite, except for start_vertex.
    distances = [float('inf')] * (num_vertices+1) # +1 optional; depends on zero-indexed
    distances[start_vertex] = 0
    
    # We only want to visit each vertex once.
    visited: set[int] = set()

    # Use a heap to iteratively pop the shortest distance vertex, 
    # until all vertices are visited
    h = []
    heapq.heappush(h, (0, start_vertex))

    # O(v): While there are still unvisited vertices...
    while len(h) > 0:
        # O(log v): Pop the next shortest distance vertex
        cur_dist, vertex = heapq.heappop(h)
        
        # O(1): Get the vertex's edges and mark the vertex as visited
        edges = adjacency[vertex]
        visited.add(vertex)
        
        # O(e): For every edge...
        for edge in edges:
            [dest_vertex, distance] = edge

            # If the vertex is visited, or we already found a shortest distance, 
            # ignore the edge
            if dest_vertex in visited or distances[dest_vertex] <= cur_dist + distance:
                continue

            # O(log v): Store the shortest distance and add it to the heap, 
            # so that we visit it later
            distances[dest_vertex] = cur_dist + distance
            heapq.heappush(h, (distances[dest_vertex], dest_vertex))
        
    return distances

🤔 adjacency list? wtf?

It contains a list of “Going from Vertex A to Vertex B requires X cost”. In the code example it’s a dict[FromVertex, list[tuple[ToVertex, Cost]]], but the tuple is simplified as a list. It can be structured differently: could be a matrix.

🧠 Pro tips!

When exercise involves a graph, or a shortest path, or a minimum cost, always think of Dijkstra!
Note that it calculates minimum distance from start_vertex to ALL vertices!
To think about TC: E*logV + V*logV because we put ~all edges and ~all vertices on the heap!

Done 🎉🎉🎉

Appendix: Other tutorials online

Leetcode Solutions: Dijkstra pattern for many exercises

Dijkstra’s Algorithm | LeetCode The Hard Way: This tutorial explains the overview, implementation, and suggested problems of Dijkstra’s algorithm with C++ code snippets.

A guide to Dijkstra’s Algorithm - LeetCode Discuss: This tutorial provides a detailed explanation and intuition behind Dijkstra’s algorithm with diagrams and examples.

Network Delay Time: This problem asks you to find the time it takes for a signal to reach all nodes in a network given a list of edges with delays. You can use Dijkstra’s algorithm to find the shortest time from the source node to each node and return the maximum time among them.
Path with Maximum Probability: This problem asks you to find the path with the maximum probability of success between two nodes in a graph given a list of edges with probabilities. You can use Dijkstra’s algorithm to find the path with the maximum product of probabilities from the source node to each node and return the product for the destination node.
Cheapest Flights Within K Stops: This problem asks you to find the cheapest price from a source city to a destination city within a given number of stops using flights. You can use Dijkstra’s algorithm to find the minimum cost from the source city to each city and keep track of the number of stops along the way.